Kris i befolkningsfrågan 2025

Som av en händelse hade jag förberett ett föredrag/samtal om Kris i befolkningsfrågan för intresserade studenter på UiO, som jag höll dagen efter att det annonserades att boken numera tillhör den svenska kulturkanon™. Föredraget var en del av ett nytt initativ där forskare ger boktips till vår studenter inom nationalekonomi.

Jag kunde ha rekommenderat många andra böcker men jag fastnade för just den boken för att “befolkningsfrågan” har kommit tillbaka med full kraft. Alva och Gunnar Myrdal skrev Kris i befolkningsfrågan 1934, när svenska födslar hade fallit till en så låg nivå så att man befarade att befolkningen i Sverige skulle minska och minska.

Födelsetalen ha fallit katastrofalt. Och de fortsätta att falla: någon botten kan ännu inte skönjas. Närmast pekar utvecklingen emot en av rena miniatyrfamiljer uppburen befolkning, vilken oavbrutet minskas i en så småningom allt snabbare takt. (s. 10)

Nu, cirka nittio år senare, är vi där igen! Fødselstallsutvalget skrev i våras i sin delrapport:

I løpet av de siste 15 årene har fødselstallene falt betydelig i store deler av verden. Samlet fruktbarhetstall i Norge har falt fra 1,98 barn per kvinne i 2009 til 1,44 barn per kvinne i 2024. Målingen for 2023 på 1,40 er det laveste nivået som er målt i Norge. Dersom trenden med lave fødselstall vedvarer, vil det få store konsekvenser for befolkningens størrelse og sammensetning. (s. 5)

Min presentation av Kris i befolkningsfrågan återfinns här. I denna korta text vill jag skriva ner några andra tankar om “befolkningsfrågan”.

Ekonomin kan påverka födelsetalen, mycket

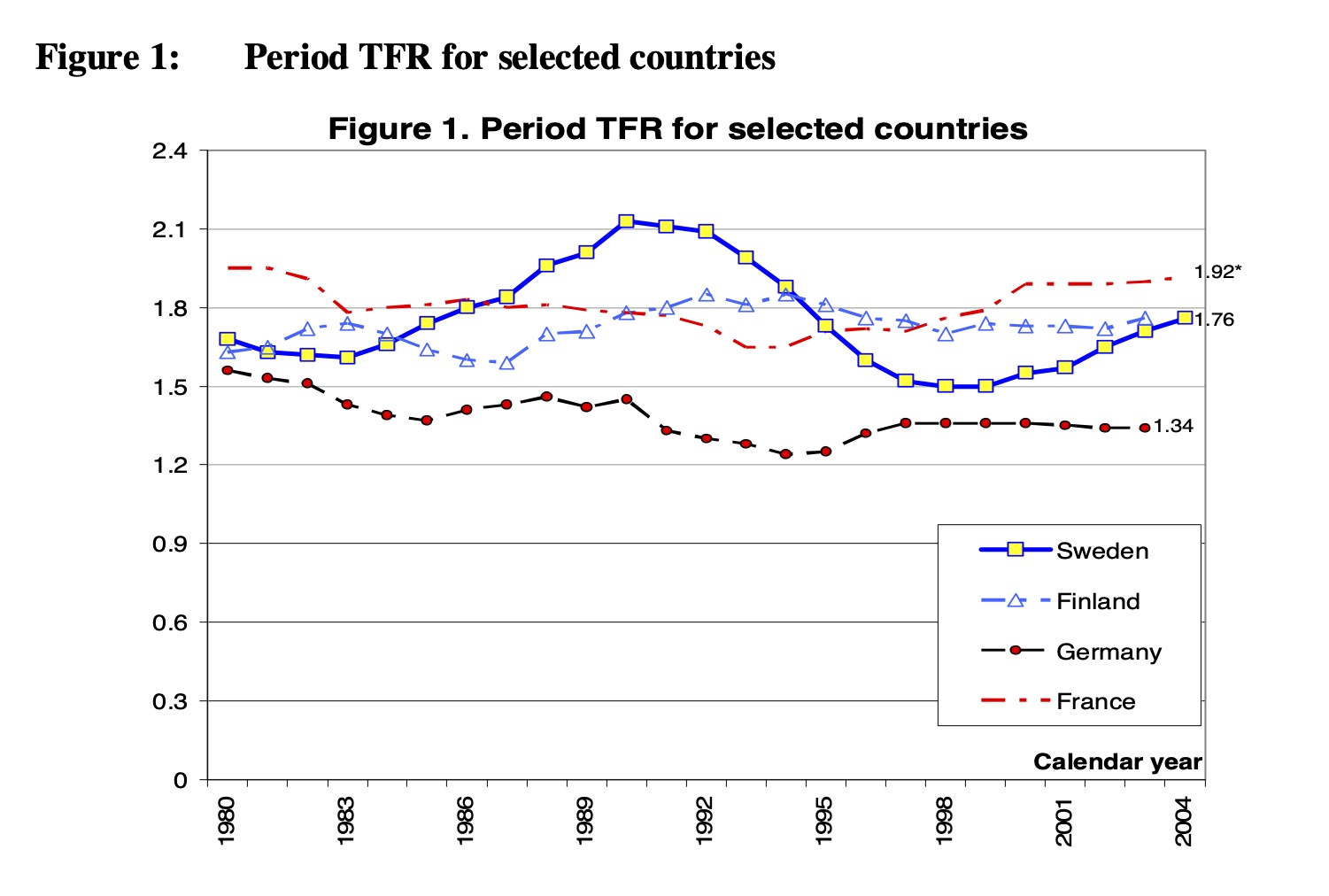
Figure 1: Summerad fruktsamhet för Sverige, Finland, Tyskland och Frankrike, från Hoem (2005).

I Figur 1, tagen från Hoem (2005), visas summerad fruktsamhet (engelska: total fertility rate) för Sverige och några till länder. Summerad fruktsamhet för ett givet år beräknas genom att justera födselstalen för just det året för demografi (ungefär: är det många eller få kvinnor i fertil ålder).

Det är slående att den svenska fruktsamheten har varierat mycket över tid, så pass mycket att den demografiska litteraturen faktiskt kallar det för en berg-och-dalbana. Det faktum att fruktsamheten kan variera så pass mycket visar att födselstalen är långt ifrån en naturlag, utan beror på mycket annat. Litteraturen lyfter fram föräldraföräkringsreformer och en bra ekonomi som orsaker till peaken i slutet av åttiotalet och den djupa ekonomiska nittiotalskrisen som orsak till det djupa fallet i fruktsamhet. När vi nu ser att fruktsamheten faller i Skandinavien och i stora delar av världen är det alltså inte något otänkbart som har skett. I Sverige har fruktsamheten varit låg förr. Vad som är nytt är att det verkar vara ett globalt fenomen att fruktsamheten faller och inte isolerat till enskilda länder.

Ekonomin påverkar födelsetalen betydligt mindre på lång sikt

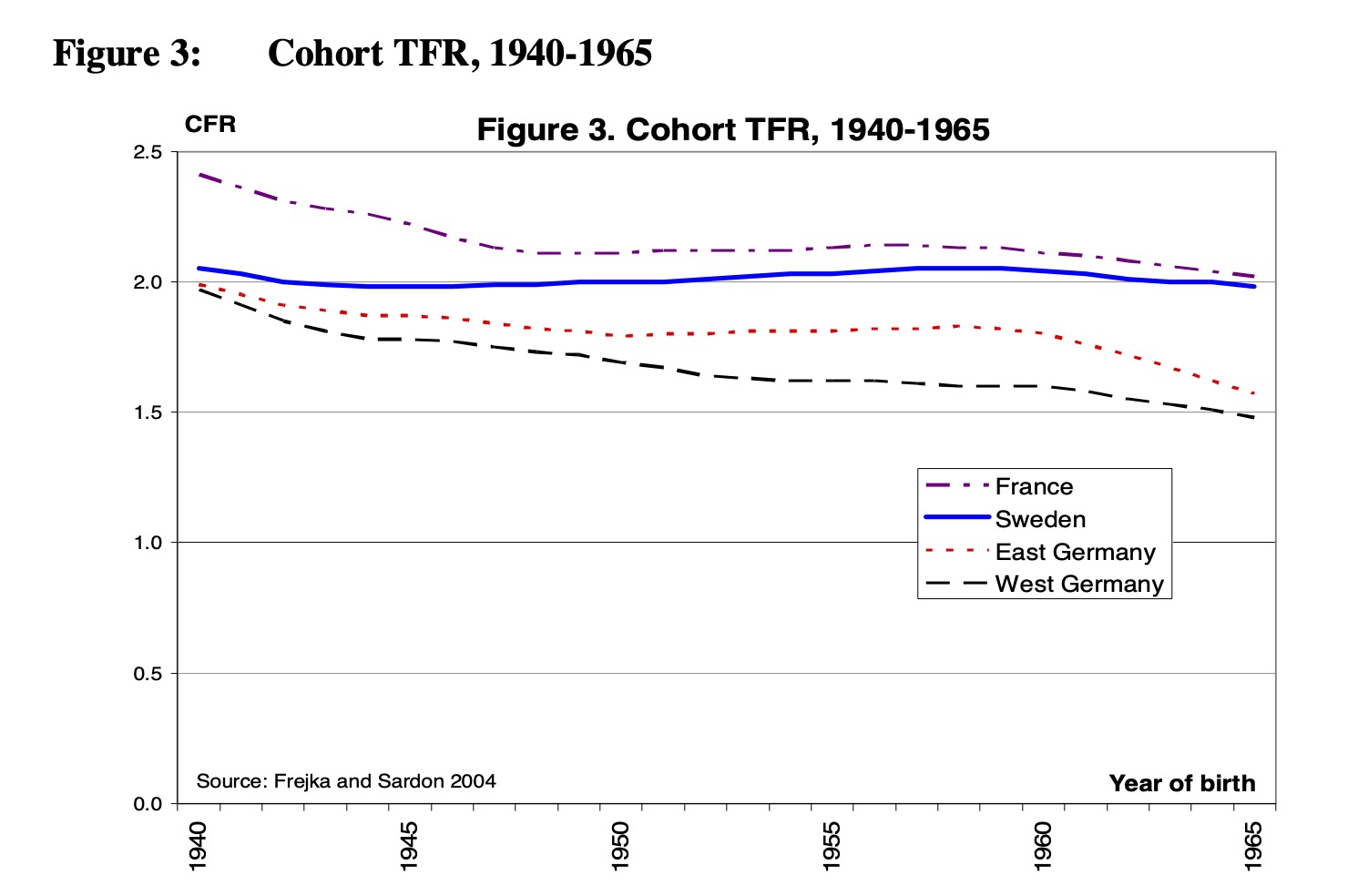
Figure 2: Kohortfruktsamhet för Sverige, Finland, Tyskland och Frankrike, från Hoem (2005).

Trots att den svenska fruktsamheten har varit att betrakta som en berg-och-dalbana så har den långsiktiga effekten på födelsetalen varit ytterst begränsad. I Figur 1 såg vi antalet födslar ett givet år, justerat för demografi. I Figur 2, också den från Hoem (2005), visas i stället antalet födslar per kvinna för en given generation (t ex kvinnor födda 1955). Trots att födslar per år kan variera kraftigt spå har, historiskt sett, antalet födslar per kvinna till slut hamnat nära 2.

Det betyder att till exempel nittiotalskrisen gjorde att par valde att skjuta upp sin familjebildning, inte att sluta ha barn. Även om grafen i Figur 2 slutar med kvinnor födda 1965 så har senare forskning visat att tvåbarnsnormen har hållt i sig fram till kvinnor födda 1975.

Men kanske det ser ut som att även kohortfruktsamheten nu är på väg ner… Vi kan bara säga något om kohortfruktsamhet när en generation i praktiken är färdiga med barnafödande, cirka vid 45 års ålder, dvs de som är födda 1980. Eventuella beteendeförändringar bland unga i dag är däremot svårtolkade: kanske de bara skjuter på barnafödande, men kanske de kommer till att ha färre barn.

Kultur eller ekonomi, vad bestämmer fruktsamheten?

Som nationalekonomi letar man gärna efter materiella förklaringar för utfall så som fruktsamhet. Samtidigt känns det, via introspektion, svårt att tänka sig att diffusa ekonomiska prognoser och ändringar i försäkringssystem skulle ha stora förändringar på våra beslut att skaffa barn. Är inte kultur en bättre förklaring för skiften i fruktsamhet? Det kan det mycket väl vara, men jag tror att en del av vad vi uppdattar som kultur också går att förstå som en komplementaritet i barnafödande.

Vill du skaffa barn, när vill du skaffa barn, och hur många barn vill du ha? En viktig komponent av svaret till dessa frågor är vad andra gör. Detta är i alla fall delvis för att ditt sociala liv förändras inte bara när du skaffar barn utan också när dina vänner skaffar barn. Att dina vänner byter ut öldrickande mot nattammande är en pushfaktor, det är inte längre lika kul att dricka öl! Att dina vänner planerar träffas vid lekplatsen är en pullfaktor, det är en bättre social miljö kring föräldraskapet om det delas med andra. Min gissning (absolut inte mer än en gissning) är att sådana här överväganden har ganska stor effekt på enskilda individers beslut. Komplementariteten i fruktsamhet inom en generation innebär att fruktsamhetsbeslut bäst förstås som en spel mellan de olika individerna.

För att vara konkret, låt mig skriva ner ett sådant stiliserat spel.

Individ $i$ får nytta av att skaffa $n_i$ barn givet av nyttofunktionen $u(n_i,\overline{n})$ där $\overline{n}$ är antalet barn som andra i individens generation skaffar. Samtidigt så är det en kostnad kopplat till att skaffa barn, $n_i$ barn in $p\cdot n_i$.

Individens maximeringsproblem är $$\underset{n_i}{max}u(n_i,\overline{n})-p{n}_i.$$

Om hen maximerar nytta (och $u$ är konkav och deriverbar i sitt första argument) så uppfyller optimalt antal barn $u_1(n_i,\overline{n})=p$ där $u_1$ är derivatan med avseende på första argumentet. Om alla individer har samma nyttofunktion så kommer de alla skaffa lika många barn, $n_i=n$, som i sin tur så klart är lika med antalet barn som andra i generationen skaffar, $n=\overline{n}$. Därför bestäms jämvikten av ekvationen $u_1(\overline{n},\overline{n})=p$.

Vad händer om vi ökar kostnaderna associerade till att skaffa barn? Om vi bara ökar kostnaderna för en individ $i$, från $p$ till $p_i$, så kommer den individen att skaffa barn enligt $u_1(n_i,\overline{n})=p_i$. För en liten förändring $d{p}_i=p_i-p$ så har vi att förändring ges av $u_{11}(\overline{n},\overline{n})d{n}_i=d{p}_i$, det vill säga att responsen av fruktsamhet till en ändring i kostnaden att skaffa barn är $$\frac{d{n}_i}{d{p}_i}=\frac{1}{u_{11}(\overline{n},\overline{n})}.$$

Funktionen $u_{11}$ fångar minskande marginalnytta av att skaffa barn och uppfyller $u_{11}<0$. Om kostnaderna ökar så minskar optimalt antal barn. Om man, via introspektion, menar att ekonomiska incitament inte spelar så stor roll så betyder det att $u_{11}$ är ett stort negativt tal (säg, -100) så att dess invers är ett litet negativt tal (-0,01) och att optimalt antal barn svarar svagt på kostnadsförändringar.

Låt oss nu i stället ändra kostnaden för alla individer. Om vi ändrar kostnaden för alla individer så kommer även jämviktsutfallet $\overline{n}$ ändras och $u_1(\overline{n},\overline{n})=p$ kommer fortfarande att hålla. För en liten förändring $dp$ gäller $(u_{11}(\overline{n},\overline{n})+u_{12}(\overline{n},\overline{n}))d\overline{n}=dp$, eller $$\frac{d\overline{n}}{dp}=\frac{1}{u_{11}(\overline{n},\overline{n})+u_{12}(\overline{n},\overline{n})}.$$ Om $u_{12}$ är positiv så är marginalnyttan av att skaffa barn ökande i om andra skaffar barn, det vill säga att vi har komplementaritet. Denna positiva term motverkar den starkt negativa termen $u_{11}$, med effekten att responsen till kostnadsförändringen potentiellt blir mycket större än om man bara hade ändrat kostnaden för en individ. Till exempel, om $u_{12}=90$ så är den aggregerade responsen till kostnadsförändringen 1/(-100+90)= - 0,1.

Det är väldigt frestande att söka mikroevidens för olika kostnadsreducerande interventioner (säg, ökat barnbidrag) genom att finna “naturliga experiment” där en (ofta liten) del av befolkningen får ta del av en reform med den kvarvarande delen av befolkningen som kontrollgrupp. Sådana studier kan estimera $u_{11}$ men inte den totala effekten $u_{11}+u_{12}$. Om komplementariten $u_{12}$ är viktig så kan mikroevidensen underskatta den samhälleliga effekten av olika interventioner.

En annan tillämpning av modellen är att om en liten del av befolkningen, av en eller annan anledning, ändrar sitt beteende så kan det få stora effekter på aggregerade utfall.

Säg att befolkningen består av $1-ϵ$ individer som fattar beslut enligt optimeringsmodellen ovan och $ϵ$ individer som av andra anledningar skaffar sig $n_{ϵ}$ antal barn. I den världen så är $\overline{n}=(1-ϵ)n+ϵn_{ϵ}$, vilket tillsammans med $u_1(n,\overline{n})=p$ ger att $n$ bestäms av $$u_1(n,(1-ϵ)n+ϵn_{ϵ})=p.$$

Låt oss nu se vad som sker om vi ändrar $n_{ϵ}$ från $\overline{n}$ med $d{n}_{ϵ}$. Jämviktsresponsen ges av $$\frac{dn}{d{n}_{ϵ}}=-\frac{ϵu_{12}(\overline{n},\overline{n})}{u_{11}(\overline{n},\overline{n})+(1-ϵ)u_{12}(\overline{n},\overline{n})}.$$ För små $ϵ$ är detta aproximativt $$\frac{dn}{d{n}_{ϵ}}=-\frac{u_{12}(\overline{n},\overline{n})}{u_{11}(\overline{n},\overline{n})+u_{12}(\overline{n},\overline{n})}ϵ.$$ I vårt räkneexempel med $u_{11}=-100$, $u_{12}=90$ så får vi $\frac{dn}{d{n}_{ϵ}}=9ϵ.$ Det vill säga, varje extra födsel i den lilla gruppen genererar nio extra födslar från den stora gruppen! En multiplikatoreffekt på tio. Även om det ser ut på mikronivå som att folk inte svarar på interventioner ($u_{11}$) så betyder inte det att en subkulturell rörelse ( $ϵ$) inte kan ha en stor effekt på födelsetalen. Det här är så klart bara ett illustrativt exempel, för att visa att komplementariteter kan ha stora effekter, inte på något sätt ett argument för att de har det.